지난번 독립변수, 종속변수, 자료분류, 가설검증방법, 유의수준에 이어서 이번에도 통계에 있어서 기본적인 것들 다중비교, 자유도 그리고 분포를 알아볼게요.
다중비교
A = B = C 라는 것을 검증할 때 흔히 하는 실수가 있습니다. 유의수준을 5%라고 하면 A = B를 검증할때도 5%이하의 오류율을 보이고 B=C를 검정할때도 5%, C=A도 5%이렇게 된다면 전체 실험의 유의수준은 5%보다 훨씬 올라가겠죠? 예를 들면, 유의수준5%는 원하는 가설을 채택했을때 그 채택한 가설이 참이될 확률을 95%이상이 되겠금하는 것이죠. 그런데 한번의 가설을 채택하는데 유의수준을 각각 책정한다면 최종적으로는 .95 x .95 x .95 = .857 밖에 맞을확률이 없는 것이네요. 그러므로 이런 다중비교를 할때는 전체유의 수준이 5%를 넘지 않도록 해야하죠. 이렇게 동시에 비교를 하기위해서 Bonferroni, Turkey, Ducan, Scheff 방법등이 있어요.
자유도
자유도는 실질적으로 독립인 값들의 개수이죠. 그렇다면 m개값의 평균을 낼때 그 자료의 자유도는 m-1이죠? m-1개의 값이 정해지면 나머지 1개는 저절로 정해지니깐요. 그리고 m x n의 교차표는 (n-1) x (m-1)의 자유도를 가집니다.
분포
동일한 실험을 여러번 하고 그 실험의 결과값을 그래프로 그려보면 특정한 모양을 띕니다. 평균값에 몰려있고 평균과 멀어질수록 적은 결과를 가지고있는 모양이 대부분이죠?
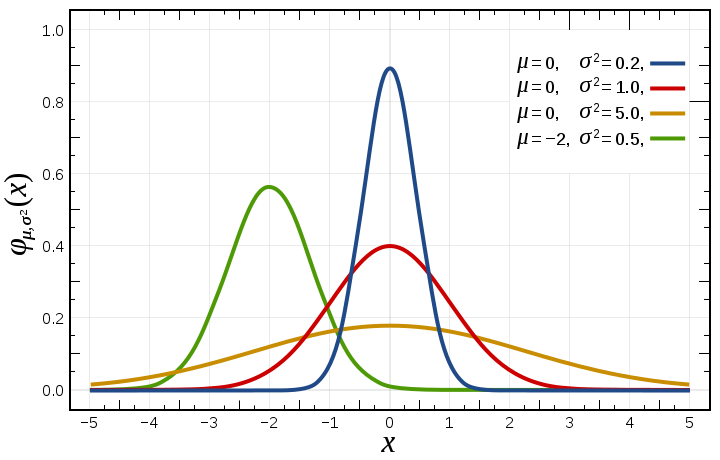 |
| 정규분포 |
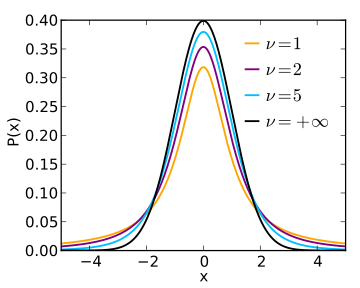 |
| T-분포 |
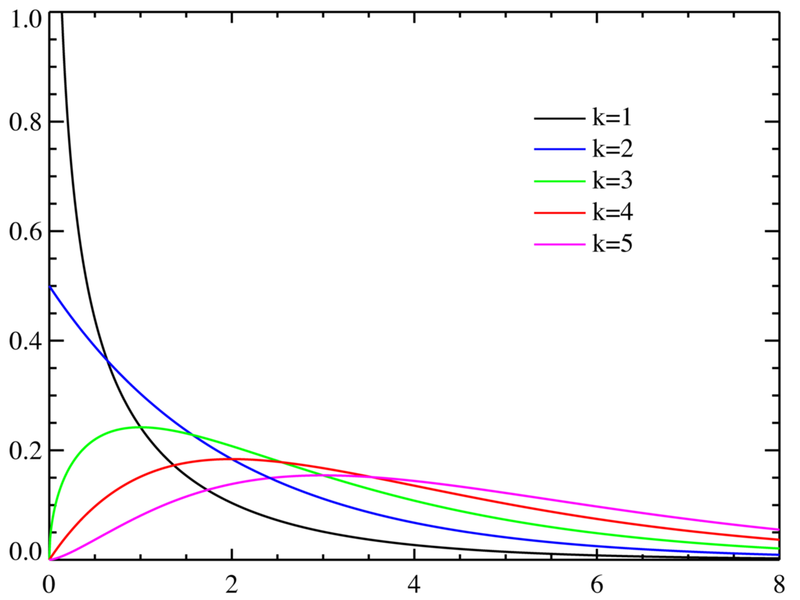 |
| 카이제곱 분포 |
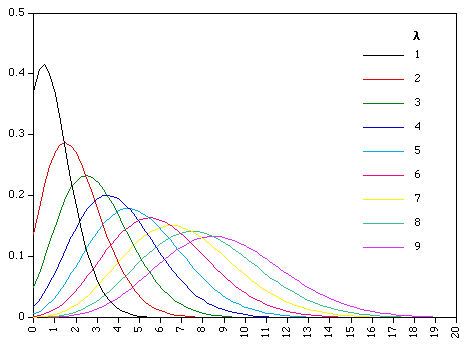 |
| 푸아송 분포 |
정말 여러 모양의 분포들이 있죠? 이런 분포들은 쓰는 상황이 각자 다릅니다. 그래서 이렇게 많이 만들어져 있겠죠? 사용하는 이유는 이러한 분포모양을 예측함으로써 많은 실험을 하지 않고도 어떤 값이 나올 확률을 알 수 있습니다. 그래프의 아래의 면적을 모두 합치면 1이됩니다. 그러므로 어떤값 이상이나 어떤값이하가 나올 확률을 면적으로 구하면 되는거죠. 그러한 면적들 값도 표로 정리되어 있어서 가져다 쓰는 방법만 알면 복잡한 적분없이도 확률예측을 할 수 있게됬어요. 고맙네요.